講座主題:Vertex stabilizers of symmetric graphs and their applications
主講人: 郭松濤
工作單位:河南科技大學
活動時間:2020年12月13日 15:40-16:30
講座地點:騰訊會議,會議ID:850 153 808
主辦單位:煙臺大學數學與信息科學學院
內容摘要:
A graph, with a group 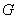 of its automorphism, is said to be
of its automorphism, is said to be 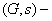 transitive, if G is transitive on
transitive, if G is transitive on 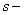 arcs but not on
arcs but not on 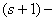 arcs of the graph. Let X be a connected
arcs of the graph. Let X be a connected 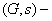 transitive graph, and let
transitive graph, and let 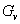 be the vertex stabilizer of a vertex
be the vertex stabilizer of a vertex 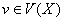 in
in 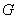 . In 1980, Djokovic and Miller gave the exact structure of
. In 1980, Djokovic and Miller gave the exact structure of 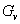 for the cubic case, and Weiss and Potocnik gave such structure for the tetravalent case. In this talk, we will discuss the structure of
for the cubic case, and Weiss and Potocnik gave such structure for the tetravalent case. In this talk, we will discuss the structure of 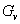 for the pentavalent and hexavalent cases, and give the idea of the main proof. Also, with the similar method, we can get such structures for the valency 7 and 8.
for the pentavalent and hexavalent cases, and give the idea of the main proof. Also, with the similar method, we can get such structures for the valency 7 and 8.
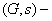 transitive graph is also simply called symmetric graph or arc-transitive graph. A graph is called edge-primitive if the full automorphism group of the graph is primitive on edges. The structure of the vertex stabilizer
transitive graph is also simply called symmetric graph or arc-transitive graph. A graph is called edge-primitive if the full automorphism group of the graph is primitive on edges. The structure of the vertex stabilizer 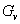 plays an important role in the study of
plays an important role in the study of 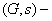 transitive graph. As we all known that except for a star graph, all the edge-primitive graphs are arc-transitive. We will introduce the method about how to use the structure of
transitive graph. As we all known that except for a star graph, all the edge-primitive graphs are arc-transitive. We will introduce the method about how to use the structure of 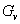 to determine the edge-primitive graphs with small valencies, and also some symmetric graphs of certain order and valency.
to determine the edge-primitive graphs with small valencies, and also some symmetric graphs of certain order and valency.
主講人介紹:
郭松濤,副教授。2009年廣西大學碩士畢業,導師徐尚進教授。2012年北京交通大學博士畢業,導師馮衍全教授。現就職于河南科技大學-數學與統計學院,從事代數圖論、置換群論和組合網絡等方面的研究。主持國家自然科學青年基金1項,河南科技大學青年學術技術帶頭人培育項目1項。在J.Combin.Theory B, J. Algebraic Combin., Electronic J. Combin., Discrete Math., Algebra Colloquium, Acta Math. Appl. Sinica English Series等國內外著名期刊上發表論文30余篇.